What Is Curve?
Curves are generally the horizontal and/or vertical bends that are usually used on highways and railways when it is necessary to change the alignment of the route. when two points are located at different levels, it becomes necessary to give a curve.
This curve usually helps to connect the points lying at different levels in such a way that the vehicles moving on that route could move with ease, safety, and comfort. A proper alignment or a curve can provide smoother movement of vehicles from one point to another, located at different levels.
A curve is introduced at the intersection of two straights to effect a gradual change in the direction. This change in direction may be in a horizontal plane or a vertical plane. So the curve is provided to the route according to its direction, i.e. either in a vertical plane or in a horizontal plane, respectively.
Types Of Curves In Surveying
Curves in surveying are classified into two main types. They are as follows:-
- Horizontal curves
- Vertical curves
1. Horizontal Curves
A horizontal curve is provided where two straight lines intersect with each other in a horizontal plane. When a curve is given in a horizontal plane, it is known as a horizontal curve. The horizontal curves are further divided as follows:
- Simple curve
- Compound curve
- Reverse curve
- Transition curve
- Combined curve
a) Simple Curve
A simple curve is a single arc of a circle, which is tangential to both the straight lines of the route. There are a few elements of a simple circular curve discussed below.

Back Tangent: The line of a tangent before the beginning of the curve is known as a back tangent.
Forward Tangent: The tangent line after the finishing of the curve is known as the forward tangent.
Point Of Intersection: A point where the back tangent and the forward tangent intersects, is known as the point of intersection.
Intersection Angle: The angle between the back and the forward tangent is known as intersection angle.
Angle Of Deflection: An angle through which the forward tangent deflects is known as angle of deflection.
Point of curvature: A point at the beginning of the curve, where the alignment changes the tangent into a curve, is known as point of curvature.
Point Of Tangency: A point at the end of the curve, where the curve changes into the tangent, is known as point of tangency.
Tangent distance: The distance between the point of curvature and point of intersection is known as the tangent distance.
Length Of Curve: The total length of curve from the point of curvature to the point of intersection is known as the length of curve.
Long Chord: A chord joining the point of curvature and the point of tangency, is known as the long chord.
Normal Chord: A chord between two successive pegs on the curve, is known as a normal chord.
Sub-chord: A chord shorter than the normal chord is known as a sub-chord.
Mid-ordinate: The distance between the midpoint of curve and the midpoint of the long chord, is known as mid-ordinate.
External Distance: The distance between the point of intersection and the midpoint of the curve, is the external distance.
b) Compound Curve
A compound curve comprises two or more circular arcs of different radii with their centers of curvature on the same side of the common tangent. It is where the cutting and filling of soil is to be avoided. Compound curves are necessary whenever the space restrictions rule out a signal circular curve and when there are property boundaries.

c) Reverse Curve
A curve consisting of two circular arcs of similar or different sizes radii having their centres on opposite sides of the common tangent at the point of reverse curvature is known as a reverse curves reverse curve is also known as a serpentine curve or S-curve due to its shape. Reverse curves are used to connect two parallel roads or railway lines. It is generally used when two lines intersect at a very small angle.
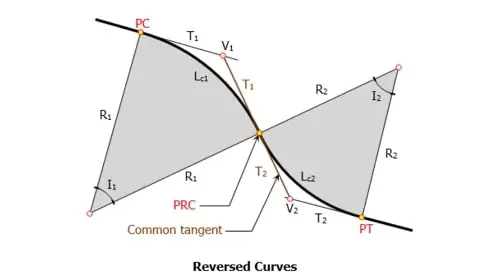
Reverse curves are best suited for hilly terrains and the highways used for relatively low-speed vehicles. Reverse curves are not advisable to use on the highways and railways which are meant for high-speed traffic movement because of the following reasons:
i) A sudden change in direction can be dangerous for vehicles.
ii) A sudden change in curvature and direction reduces the life of vehicles and also provides discomfort to the people traveling on that route.
iii) If the driver is careless, it may cause the vehicle to overturn over a reverse curve.
d) Transition Curve
It is a curve of varying radius. The value of the radius of this type of curve varies from infinity to a certain fixed value. It provides a gradual change from the straight line to the circular curve and again from the circular curve to a straight line. It is usually provided on both ends of a circular curve. The transition curves are provided on roads and railways to lessen the discomfort at the sudden change in curvature at the junction of a straight line and a curve.

A transition curve has the following advantages:
i) Transition curve reduces the probability of overturning vehicles at the junction of the straight and the curve.
ii) It gives comfort to the passengers.
iii) It allows higher speeds for vehicles at the curves.
iv) Transition curve reduces the wear and tear of the rail section, occurring due to unusual friction at point of curve.
v) Combined Curve
The combination of a simple circular curve and a transition curve, is known as a combined curve. Combined curves are mostly preferred in highways and railways.
When transition curves are provided at both ends of a circular curve, the curve formed is known as a combined or a complete curve.

2. Vertical curves
Vertical curves are usually provided when a highway or a railway crosses a ridge or a valley. Vertical curves are provided when there is a difference of level between two points. So to make the movement easy between these points, a vertical curve is provided. It makes the transition of the vehicle smooth and comfortable.
There are two main types of vertical curves.
- Summit curve, and
- Valley curve.
a. Summit Curve
A vertical curve having its convexity in the upwards direction is known as a summit curve.

Summit curves are usually provided in the following cases:
i) When an upgrade is followed by a downgrade,
ii) When a steeper upgrade is followed by a milder upgrade, and
iii) When a milder downgrade is followed by a steeper upgrade.
b. Sag Curve Or Valley Curve
A vertical curve having its convexity in the downwards direction or when it is concave upwards is known as a valley curve. It is also known as sag curve.

A sag curve or a valley curve is usually formed in the following cases:
i) When a downgrade is followed by an upgrade,
ii) When a steeper downgrade is followed by a milder upgrade, and
iii) When a milder upgrade is followed by a steeper upgrade.